[AI] Perceptron
🎯 퍼셉트론 학습 알고리즘

Python으로 퍼셉트론 구현하기
import numpy as np
def step_func(t): # 퍼셉트론의 활성화 함수
if t > 0.: return 1
else: return 0
X = np.array([ # 훈련 데이터 세트
[0, 0, 1], # 맨 끝의 1은 바이어스를 위한 입력 신호 1이다.
[0, 1, 1],
[1, 0, 1],
[1, 1, 1]
])
y = np.array([0, 0, 0, 1]) # 정답을 저장하는 넘파이 행렬
W = np.zeros(len(X[0])) # 가중치를 저장하는 넘파이 행렬def perceptron_fit(X, Y, epochs=10): # 퍼셉트론 학습 알고리즘 구현
global W
eta = 0.2 # 학습률
for t in range(epochs):
print("epoch=", t, "======================")
for i in range(len(X)):
predict = step_func(np.dot(X[i], W))
error = Y[i] - predict # 오차 계산
W += eta * error * X[i] # 가중치 업데이트
print("현재 처리 입력=", X[i], "정답=", Y[i], "출력=", predict, "변경된 가중치=", W)
print("================================")def perceptron_predict(X, Y): # 예측
global W
for x in X:
print(x[0], x[1], "->", step_func(np.dot(x, W)))
perceptron_fit(X, y, 6)
perceptron_predict(X, y)결과

sklearn으로 퍼셉트론 구현
from sklearn.linear_model import Perceptron
# 샘플과 레이블.
X = [[0,0],[0,1],[1,0],[1,1]]
y = [0, 0, 0, 1]
# 퍼셉트론 생성. tol는 종료 조건.
# random_state는 난수의 seed.
clf = Perceptron(tol=1e-3, random_state=0)
# 학습.
clf.fit(X, y)
# 테스트.
print(clf.predict(X))
🎯 다중 퍼셉트론 (MLP : Multilayer Perceptron)
: 입력층과 출력층 사이에 은닉층(hidden layer)을 가지고 있는 퍼셉트론

활성화 함수
: 입력 신호의 총합을 출력 신호로 변환하는 함수
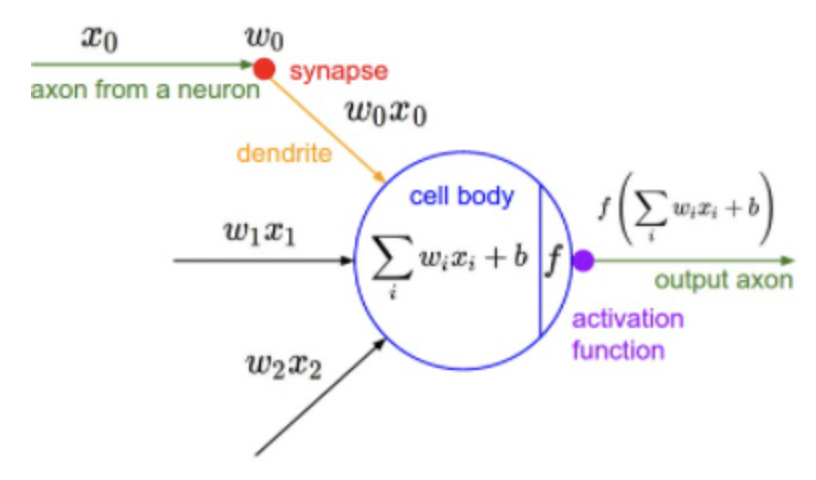
- 신경망의 활성화 함수는 비선형이어야 한다.
(선형 함수일 경우 아무리 층이 많아져도 하나의 함수로 대치될 수도 있기 때문에 여러 층을 쌓는 효과를 볼 수 없다.)
🎯활성화 함수 종류
1. 시그모이드(sigmoid) 함수

- 기울기 소멸 문제 (Vanishing Gradient Problem)
: 시그모이드(sigmoid)함수에서는 x의 절댓값이 클수록 기울기는 0에 수렴하게 된다. 이는 역전파 중에 이전의 기울기와 현재 기울기를 곱하면서 점점 기울기가 사라지게 된다. -> 신경망의 학습 능력이 제한되는 포화(saturation)가 발생
<Python Code>
import numpy as np
import matplotlib.pylab as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
#그래프 그러보기
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()
2. ReLU (Rectified Linear Unit) 함수

<Python Code>
def relu(x):
return np.maximum(0,x)
#그래프 그러보기
x = np.arange(-10, 10)
y = relu(x)
plt.plot(x, y)
plt.ylim(-1, 10.1)
plt.show()
3. tanh 함수

<Python Code>
def tanh(x):
return (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))
#그래프 그러보기
x = np.arange(-10.0, 10.0, 0.1)
y = tanh(x)
plt.plot(x, y)
plt.ylim(-1.1, 1.1)
plt.show()
Python으로 MLP 순방향 패스 구현하기
import numpy as np
# sigmoid 함수
def actf(x):
return 1/(1+np.exp(-x))
# sigmoid 함수의 미분치
def actf_deriv(x):
return x*(1-x)
# 입력유닛의 개수, 은닉유닛의 개수, 출력유닛의 개수
inputs, hiddens, outputs = 2, 2, 1
learning_rate=0.2
# 훈련 샘플과 정답
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
T = np.array([[0], [1], [1], [0]])W1 = np.array([[0.10, 0.20], [0.30, 0.40]])
W2 = np.array([[0.50], [0.60]])
B1 = np.array([0.1, 0.2])
B2 = np.array([0.3])
# 순방향 전파 계산
def predict(x):
layer0 = x # 입력을 layer0에 대입
Z1 = np.dot(layer0, W1)+B1 # 행렬의 곱을 계산
layer1 = actf(Z1) # 활성화 함수를 적용한다.
Z2 = np.dot(layer1, W2)+B2 # 행렬의 곱을 계산한다.
layer2 = actf(Z2) # 활성화 함수를 적용한다.
return layer0, layer1, layer2def test():
for x, y in zip(X, T):
layer0, layer1, layer2 = predict(x)
print(x, y, layer2)
test()
# 학습이 없으므로 난수만 출력
🎯 손실 함수 (Loss function)
지도학습 시 알고리즘이 예측한 값과 실제 정답의 차이를 비교하기 위한 함수
'학습 중에 알고리즘이 얼마나 잘못 예측하는 정도'를 확인하기 위한 함수로써 최적화(Optimization)를 위해 최소화하는 것이 목적인 함수

- L : 손실 함수
- arg min : arguments of minimum을 축약한 수학적 표현으로, 목적 함수를 최소화하는 입력값을 찾는 역할 (목적함수 = L)
- x : 학습 데이터의 입력값
- y : 학습 데이터의 정답
- Θ : 알고리즘 학습 시 사용되는 모든 파라미터의 벡터
- ~Θ : 추정된 최적의 파라미터
🎯 평균 제곱 오차 (MSE)
- 예측값과 정답 간의 평균 제곱 오차

🎯경사하강법
- 목표 : 손실함수 값을 최소로 하는 가중치를 찾는 것
- 신경망 학습 문제 -> 최적화 문제(optimization)
- 손실함수를 가중치로 미분한 값이 양수 -> 가중치를 감소
- 손실함수를 가중치로 미분한 값이 음수 -> 가중치를 증가
<Python Code>

손실함수 : y = (x-3)^2 +10
gradient : y' = 2x - 6
x = 10
learning_rate = 0.2
precision = 0.00001
max_iterations = 100
# 손실함수를 람다식으로 정의한다.
loss_func = lambda x: (x-3)**2 + 10
# gradient를 람다식으로 정의한다. 손실함수의 1차 미분값이다.
gradient = lambda x: 2*x-6
# gradient 강하법
for i in range(max_iterations):
x = x - learning_rate * gradient(x)
print("손실함수값(", x, ")=", loss_func(x))
print("최소값 = ", x)
2차원 gradient 시각화 Python Code
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(-5, 5, 0.5)
y = np.arange(-5, 5, 0.5)
X, Y = np.meshgrid(x,y) # 참고박스
U = -2*X # gradient의 음수
V = -2*Y
plt.figure()
Q = plt.quiver(X, Y, U, V, units='width')
plt.show()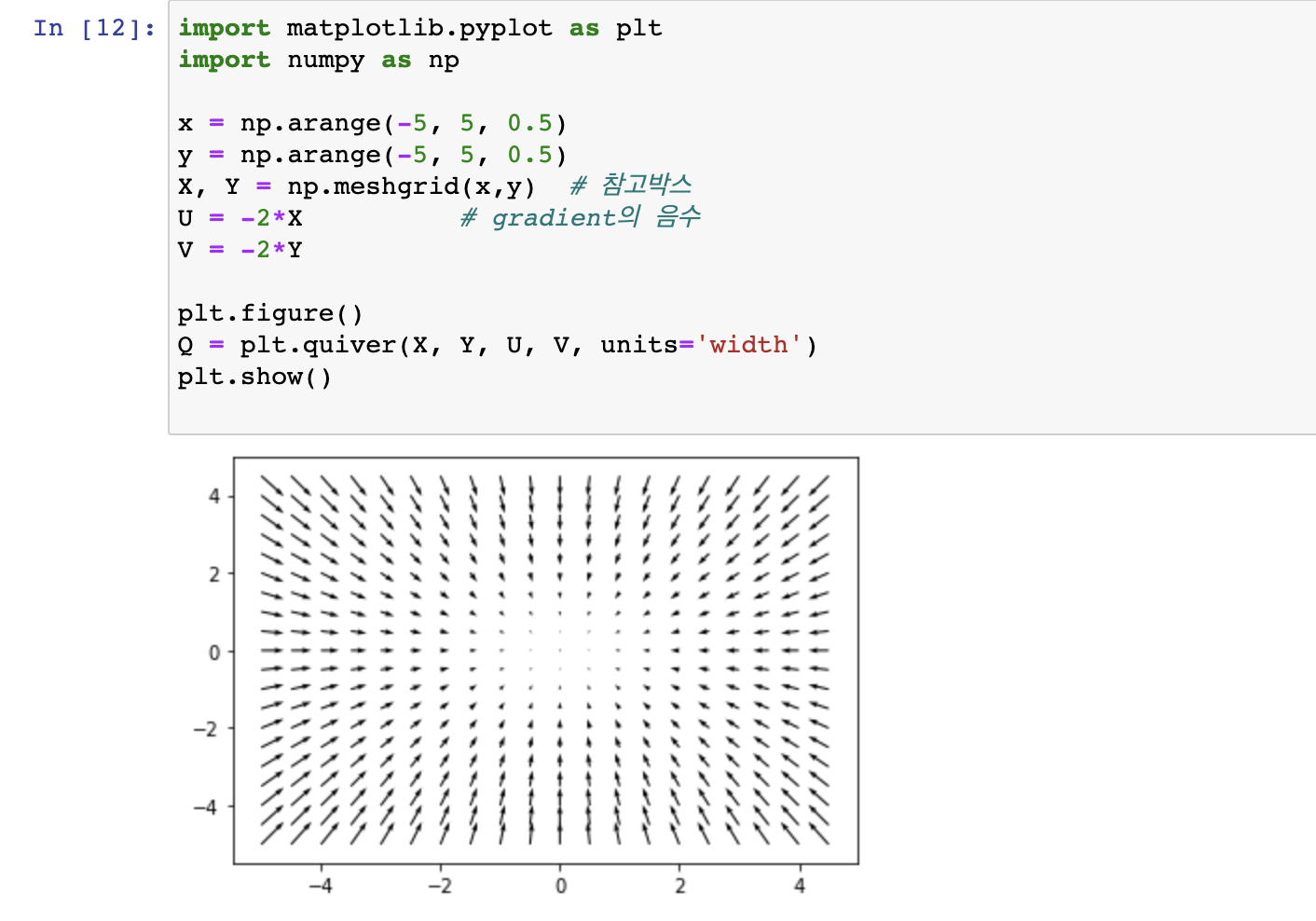
🎯 역전파 학습 알고리즘 (Back Propagation)
: input과 output을 알고 있는 상태(supervised learning)에서 신경망을 학습시키는 방법
과정
1. 입력이 주어지면 순방향으로 계산하여 출력을 계산
2. 실제 출력과 우리가 원하는 출력 간의 오차를 계산
3. 이 오차를 역방향으로 전파하면서 오차를 줄이는 방향으로 가중치를 변경

3-1. 가중치와 바이어스를 0부터 1 사이의 난수로 초기화
3-2. 수렴할 때까지 모든 가중치에 대해 다음을 반복
- 손실함수 E의 gradient 를 계산

- 역전파 알고리즘의 유도 : 미분의 chain rule 이용
Dynamic Programming (동적 계획법)
: 하나의 큰 문제를 여러 개의 작은 문제로 나누어서 그 결과를 저장해 다시 큰 문제를 해결할 때 사용하는 것 (문제해결 패러다임)
numpy를 이용한 MLP 구현
import numpy as np
# sigmoid 함수
def actf(x):
return 1/(1+np.exp(-x))
# sigmoid 함수의 미분치
def actf_deriv(x):
return x*(1-x)
# 입력유닛의 개수, 은닉유닛의 개수, 출력유닛의 개수
inputs, hiddens, outputs = 2, 2, 1
learning_rate=0.2
# 훈련 샘플과 정답
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
T = np.array([[1], [0], [0], [1]])순방향 전파 구현
W1 = np.array([[0.10,0.20], [0.30,0.40]])
W2 = np.array([[0.50],[0.60]])
B1 = np.array([0.1, 0.2])
B2 = np.array([0.3])
# 순방향 전파 계산
def predict(x):
layer0 = x # 입력을 layer0에 대입한다.
Z1 = np.dot(layer0, W1)+B1 # 행렬의 곱을 계산
layer1 = actf(Z1) # 활성화 함수를 적용한다.
Z2 = np.dot(layer1, W2)+B2 # 행렬의 곱을 계산한다.
layer2 = actf(Z2) # 활성화 함수를 적용한다.
return layer0, layer1, layer2오차 역전파 구현
# 역방향 전파 계산
def fit():
global W1, W2, B1, B2 # 외부에 정의된 변수를 변경해야 한다.
for i in range(90000): # 9만번 반복한다.
for x, y in zip(X, T): # 학습 샘플을 하나씩 꺼낸다.
x = np.reshape(x, (1, -1)) # 2차원 행렬로 만든다. 1
y = np.reshape(y, (1, -1)) # 2차원 행렬로 만든다.
layer0, layer1, layer2 = predict(x) # 순방향 계산
layer2_error = layer2-y # 오차 계산
layer2_delta = layer2_error*actf_deriv(layer2) # 출력층의 델타 계산
layer1_error = np.dot(layer2_delta, W2.T) # 은닉층의 오차 계산 2
layer1_delta = layer1_error*actf_deriv(layer1) # 은닉층의 델타 3
W2 += -learning_rate*np.dot(layer1.T, layer2_delta) # 4
W1 += -learning_rate*np.dot(layer0.T, layer1_delta)
B2 += -learning_rate*np.sum(layer2_delta, axis=0) # 5
B1 += -learning_rate*np.sum(layer1_delta, axis=0)
def test():
for x, y in zip(X, T):
x = np.reshape(x, (1, -1)) # 하나의 샘플을 꺼내서 2차원 행렬로 만든다.
layer0, layer1, layer2 = predict(x)
print(x, y, layer2) # 출력층의 값을 출력해본다.
fit()
test()