[AI] KERAS
🎯 가중치를 변경하는 방법
1. Full batch learning

2. 온라인 학습

3. Mini batch 학습 (확률적 경사 하강법)

<Python으로 Mini batch 구현>
import numpy as np
import tensorflow as tf
# 데이터를 학습 데이터와 테스트 데이터로 나눈다.
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
data_size = x_train.shape[0]
batch_size = 12 # batch 크기
selected = np.random.choice(data_size, batch_size) # batch 크기만큼 랜덤하게 선택
print(selected)
x_batch = x_train[selected]
y_batch = y_train[selected]
<행렬을 사용한 Mini batch 구현>
🎯 경사 하강법의 종류
1. 확률적 경사 하강법 (SGD : Stochastic Gradient Descent)
- Gradient Descent를 전체 데이터(Batch)가 아닌 일부 데이터의 모음(Mini-batch)를 사용하는 방법
- 다소 부정확할 수는 있지만, 계산 속도가 훨씬 빠르기 때문에, 같은 시간에 더 많은 step을 나아갈 수 있다.
- Local Minima에 빠지지 않고 Gloval Minima에 수렴할 가능성이 높다.
- 매우 단순하고 구현이 편리하지만 상황에 따라 매우 효율이 떨어지는 경우가 많다.
- 예를 들어 비등방성(anisotropy) 함수와 같이 방향에 따라 기울기가 달라지는 함수에 대해서는 매우 비효율적이다.
- 또한 학습률(Learning rate)이 낮으면 곧장 최적화하지 못하고 지그재그로 이동하게 되면서 지역 최소값(local Minima)에 갇혀 빠져나오지 못하는 경우가 있고, 학습률이 높으면 최적화 자체를 실패할 수도 있다.

2. 모멘텀 (Momentum)
- 경사 하강법에 관성을 더해 주는 것
- 매번 기울기를 구하지만, 가중치를 수정하기 전 이전 수정 방향(+,-)를 참고하여 같은 방향으로 일정한 비율만 수정되게 하는 방법
- 가속도 역할 (gradient가 속도를 조절하는 역할을 한다.)
-> 학습속도 향상
-> Weight 변화가 oscillating(진동) 하는 것 방지

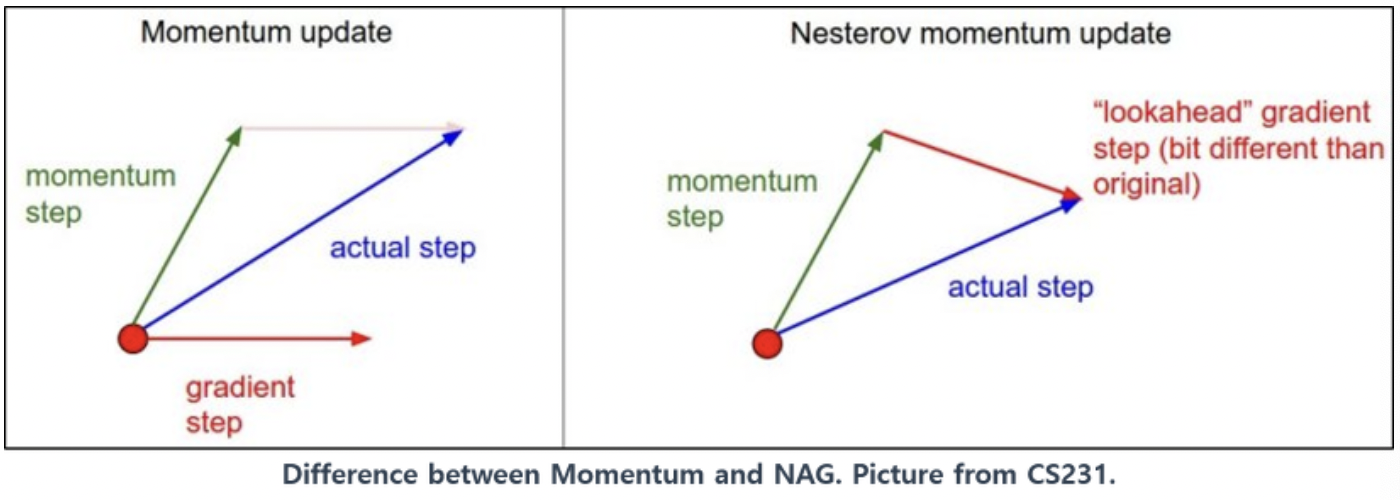
3. 네스테로프 모멘텀 (Nesterov Momemtum)
- 미래의 위치를 미리 계산 후 이동
- momentum값과 gradient값이 더해져 실제(actual) 값을 만드는 기존 모멘텀과 달리 Momentum값이 적용된 지점에서 gradient값이 계산된다.
4. Adagrad (Adaptive Gradient, 아다그리드)
- 가변 학습률을 사용하는 방법
- SGD 방법을 개량한 최적화 방법
- 주된 방법 = 학습률 감쇠 (learning rate decay)
- 학습률을 이전 단계의 기울기들을 누적한 값에 반비례하여 설정
(많이 변화하지 않은 변수들은 학습률(step size)를 크게하고, 반대로 많이 변화한 변수들에 대해서는 학습률을 적게한다.)
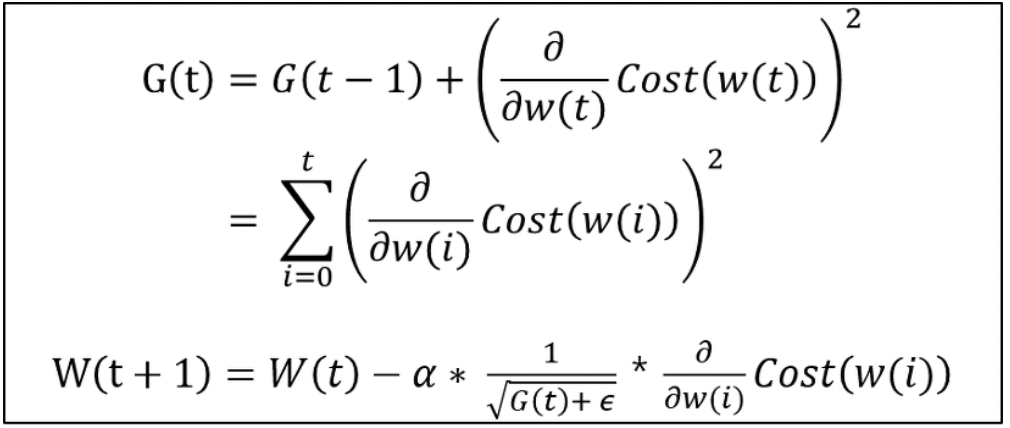
5. Adadelta (Adaptive Delta, 아다델타)
- Adagrad의 개선
- Adagrad + RMSprop + Momentum 모두를 합친 경사하강법
- Adapts learning rates based on a moving window of gradient updates/
- 처음부터 현재 시간 t까지의 모든 gradients를 더하지 않고, 최근 일정기간 동안의 gradients만 더한다.
6. RMSprop (Root Mean Square Propagation)
- Adagrad에 대한 수정판
Adagrad의 문제 : 시간이 흐를수록 update양이 작아짐
-> exponentially decaying average to discard history from the extreme past
( 극단적 과거의 역사를 버리기 위해 기하급수적으로 감소하는 평균)
- Geoffy Hinton이 제안
- Gradient 누적 대신에 지수 가중 이동 평균을 사용
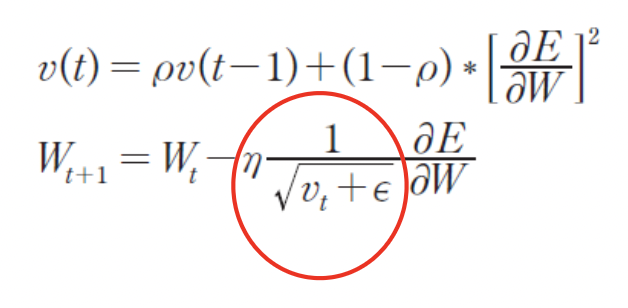
7. Adam (Adaptive Moment Estimation)
- RMSprop + Momentum
- RMSprop의 특징인 gradient의 제곱을 지수평균한 값을 사용하며 Momentum의 특징으로 gradient를 제곱하지 않은 값을 사용하여 지수평균을 구하고 수식에 활용
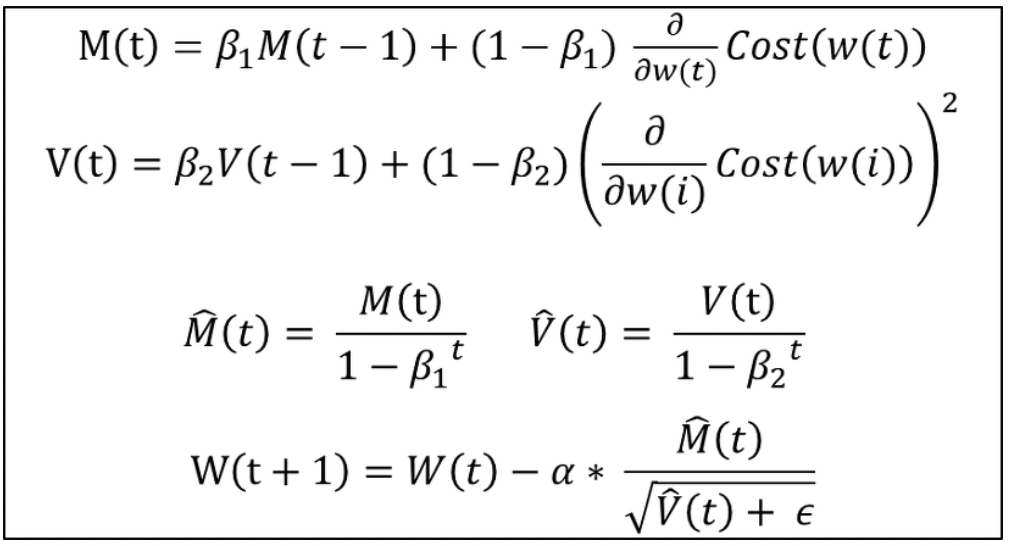
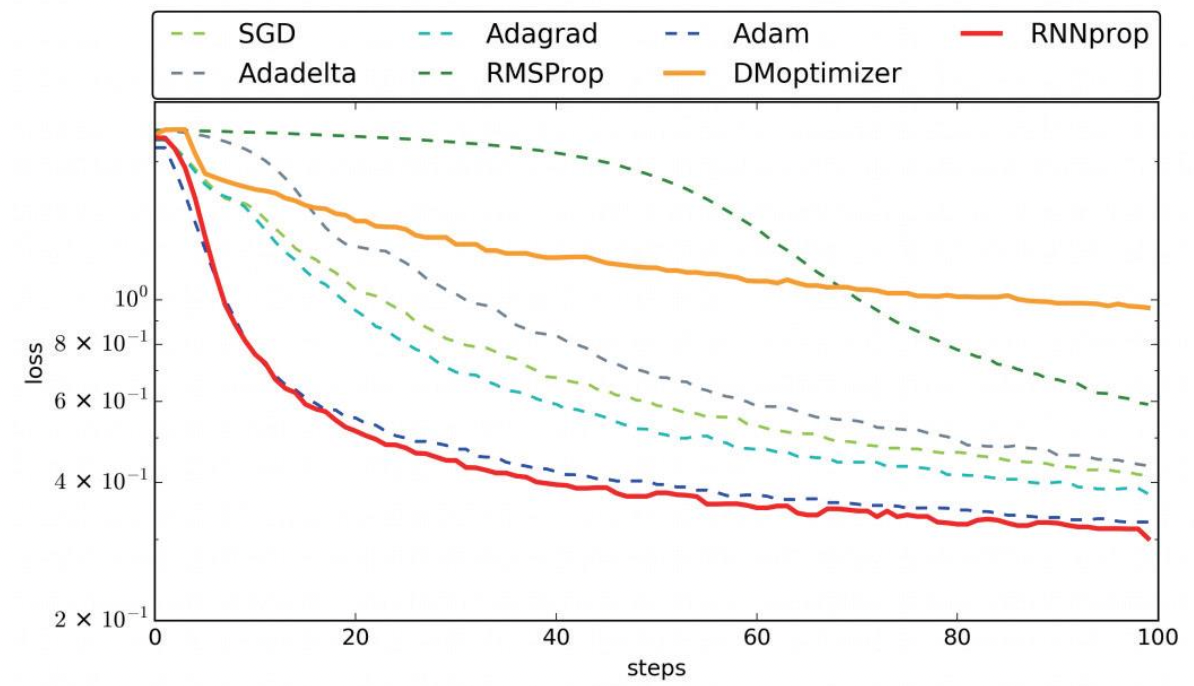
🎯 TensorFlow의 구조
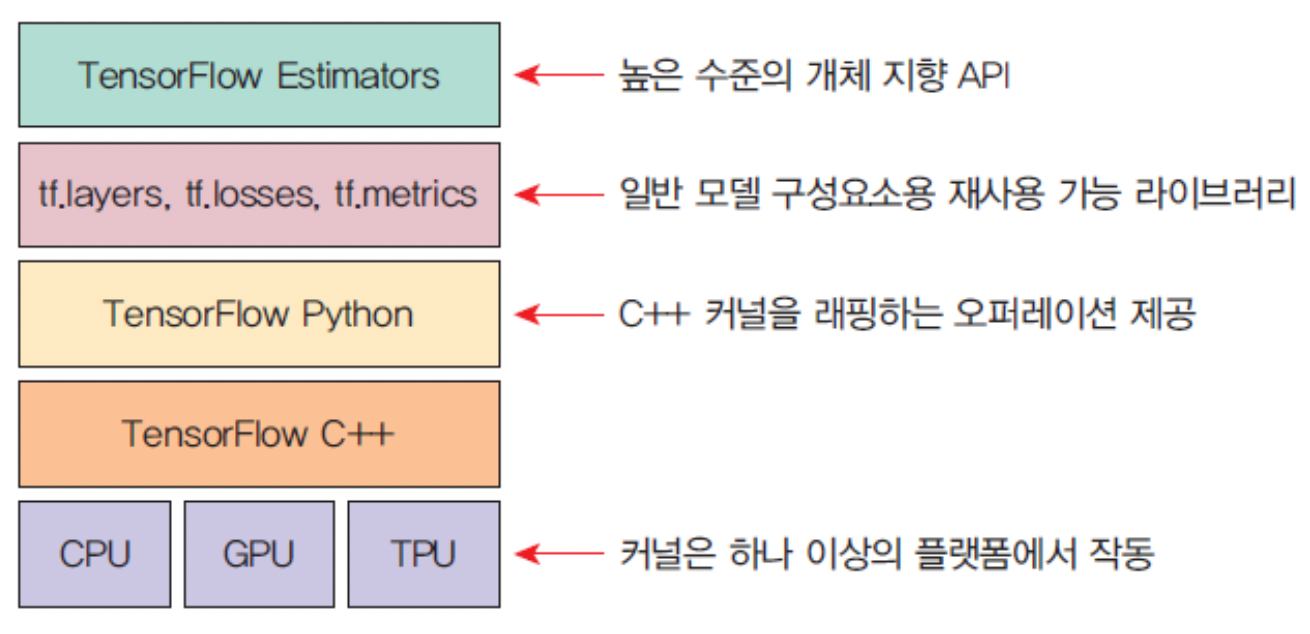
🎯 Keras
- python으로 작성된, 고수준 딥러닝 API
- 여러 가지 백엔드를 선택할 수 있으며, 가장 많이 선택되는 백엔드는 TensorFlow
- 쉽고 빠른 프로토타이핑 가능
- Feed forward 신경망, convolution 신경망과 순환 신경망은 물론, 여러가지 조합도 지원
- CPU 및 GPU에서 원활하게 실행
- Keras로 신경망을 작성하는 절차
- Keras의 핵심 데이터 구조는 모델 (model)
: layer를 구성하는 방법
- 가장 간단한 모델 유형은 Sequential 선형 스택 모델
: layer를 선형으로 쌓을 수 있는 신경망 모델
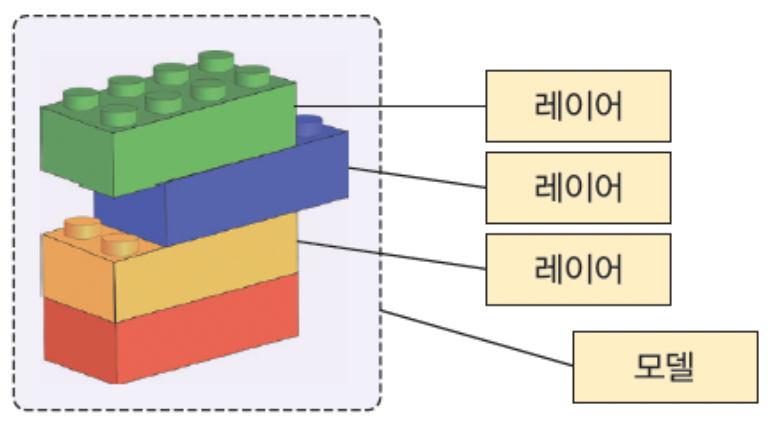
- XOR를 학습하는 MLP를 작성
model = tf.keras.models.Sequential()
# Sequential 모델을 생성
model.add(tf.keras.layers.Dense(units=2, input_shape=(2,), activation='sigmoid')) # 1.
model.add(tf.keras.layers.Dense(units=1, activation='sigmoid') # 필요한 layer를 추가
model.complie(loss='mean_squared_error', optimizer=keras.optimizers.SGD(lr=0.3))
model.fit(X, y, batch_size=1, epochs=10000) # 학습을 수행
print(model.predict(X))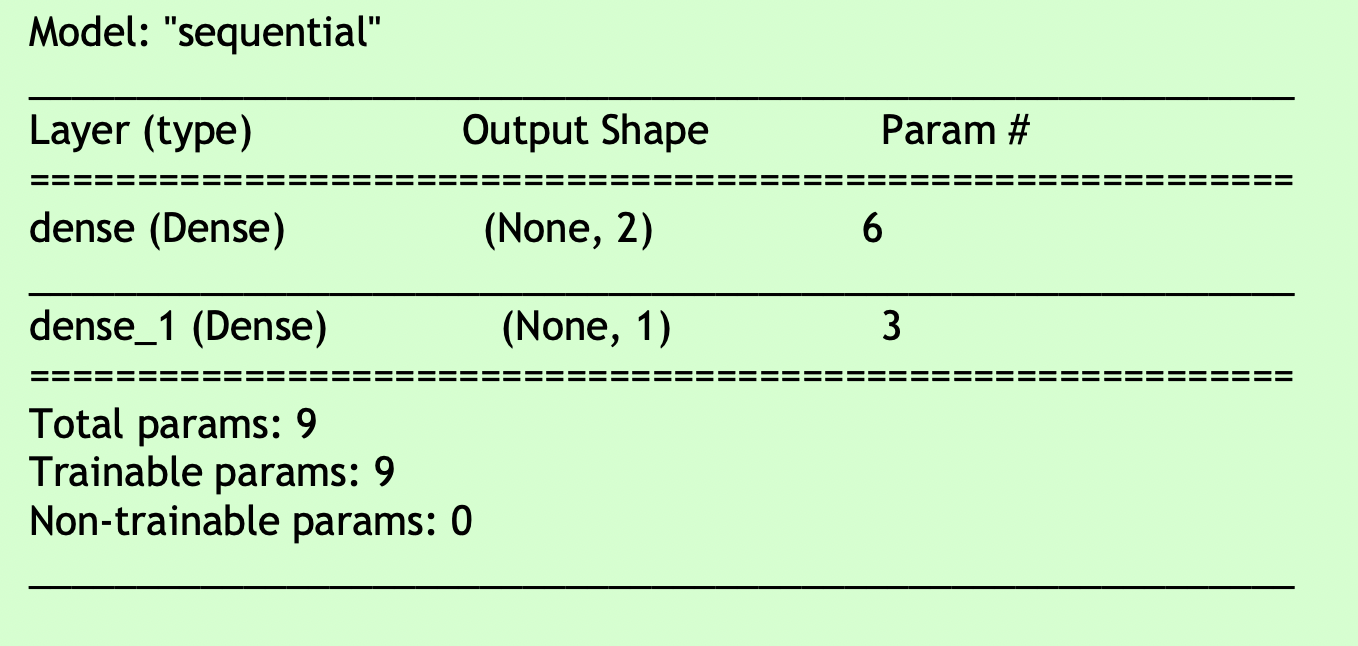

🎯 Keras를 사용하는 3가지 방법
1. Sequential 모델을 만들고 모델에 필요한 layer를 추가
model = Sequential()
model.add(Dense(units=2, input_shape=(2,), activation='sigmoid'))
model.add(Dense(units=1, activation='sigmoid'))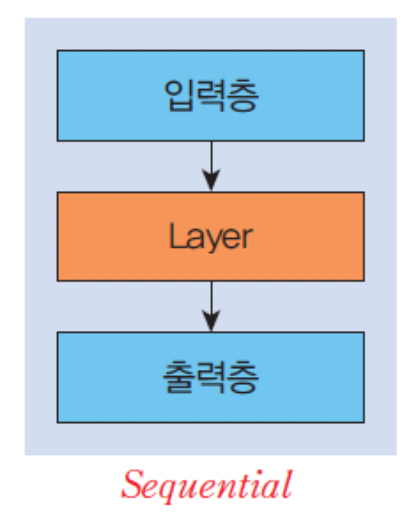
2. 함수형 API를 사용하는 방법
inputs = input(shape=(2,)) # 입력층
x = Dense(2, activation='sigmoid')(inputs) # 은닉층 1.
prediction = Dense(1, activation='sigmoid')(x). # 출력층
model = Model(inputs=inputs, outputs=prediction)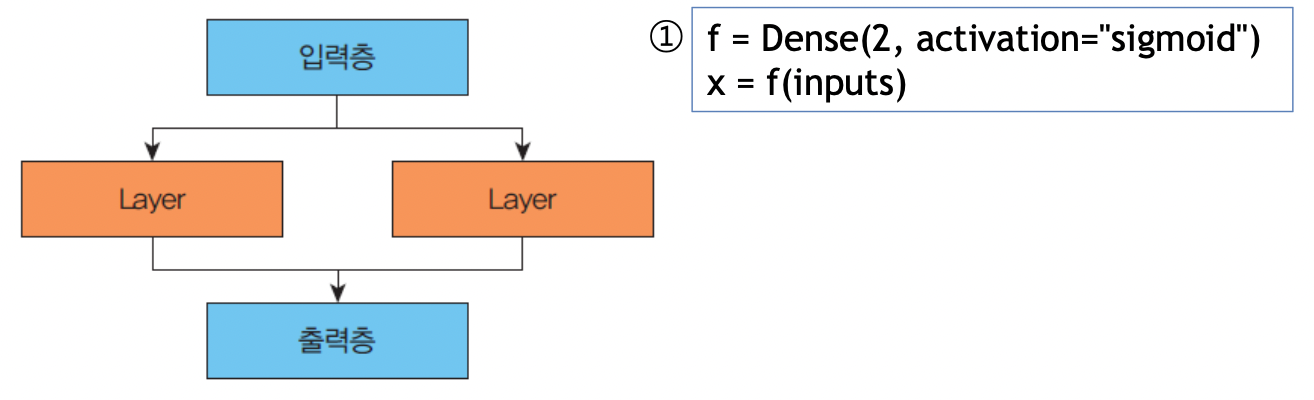
3. Model 클래스를 상속받아서 우리 나름대로의 클래스를 정의하는 방법
class SimpleMLP(Model):
def __init__(self, num_classes): # 생성자 작성
super(SimpleMLP, self).__init__(name='mlp')
self.num_classes = num_classes
self.dense1 = Dense(32, activation='sigmoid')
self.dense2 = Dense(num_classes, activation='sigmoid')
def call(self, inputs): # 순방향 호출을 구현
x = self.dense1(inputs)
return self.dense2(x)
model = SimpleMLP()
model.compile(...)
model.fit(...)49p ~ )