티스토리 뷰
🎯 선형 회귀란?
- 종속 변수 y와 한 개 이상의 독립 변수 (또는 설명 변수) X와의 선형 상관 관계를 모델링하는 회귀분석 기법
- 입력 데이터를 가장 잘 설명하는 기울기와 절편값을 찾는 문제
1. 단순 선형 회귀 분석 (Simple Linear Regression Analysis)
f(x) = wx + b
- 기울기 -> 가중치 (weight)
- 절편 -> bias
2. 다중 선형 회귀 분석 (Multiple Linear Regression Analysis)

ex)
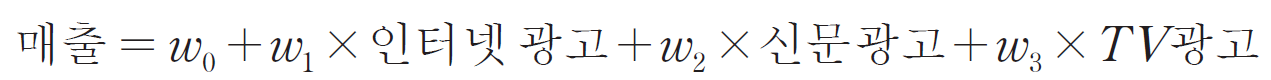
🎯 손실 함수 (loss function) / 비용 함수 (cost function)
- 직선과 데이터 사이의 간격을 제곱하여 합한 값으로 예측값과 실제값에 대한 오차를 줄이기 위해 사용


🎯선형 회귀에서 손실 함수 최소화 방법
1. 최소 제곱법 (LSM : Least Square Method)
- 단순 회귀 분석에서만 사용
y = ax + b


2. 경사 하강법 (GD : Gradient descent)
- 손실 함수가 어떤 형태라도, 매개 변수가 아무리 많아도 적용 가능한 일반적인 방법
- 점진적인 학습
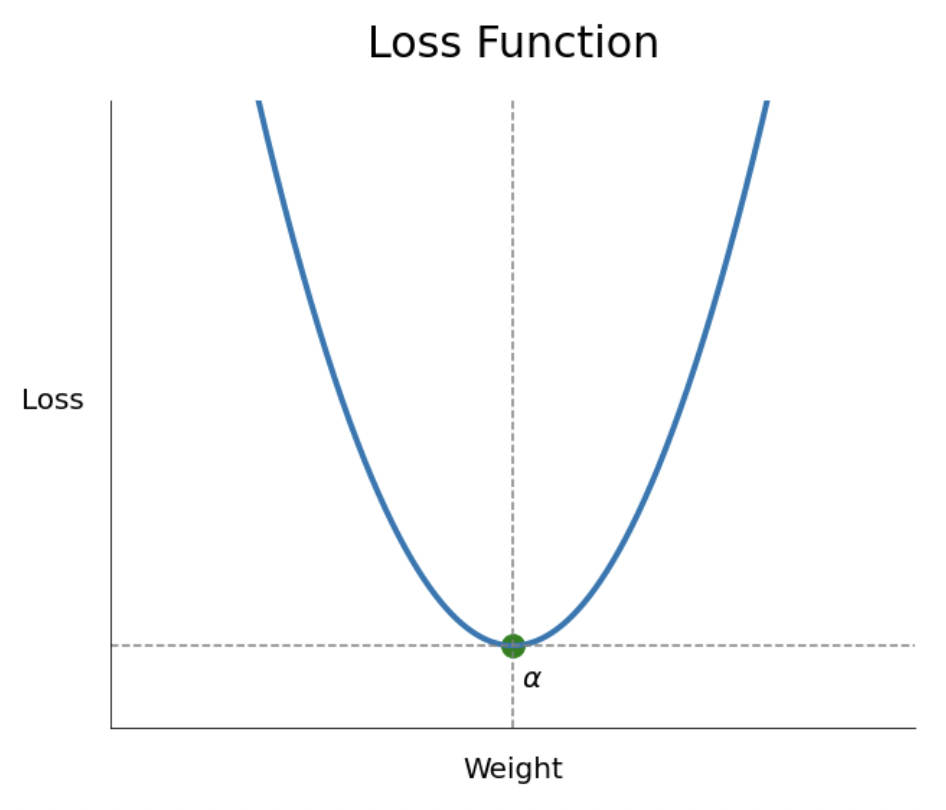

- 다음과 같은 개형의 손실함수에서 손실 함수를 최소로 만드는 점 alpha를 찾는 것
경사 하강법 과정
- 손실 함수의 랜덤 한 위치에서 기울기를 계산
-> 기울기가 0이 되는 방향으로 학습률(learning rate)만큼 점진적으로 이동해 최적의 alpha를 찾는 것
-> 위 과정은 전역 최적해를 찾기 위해 반복 수행 (다양한 랜덤한 위치에서 경사 하강법이 실시된다.)
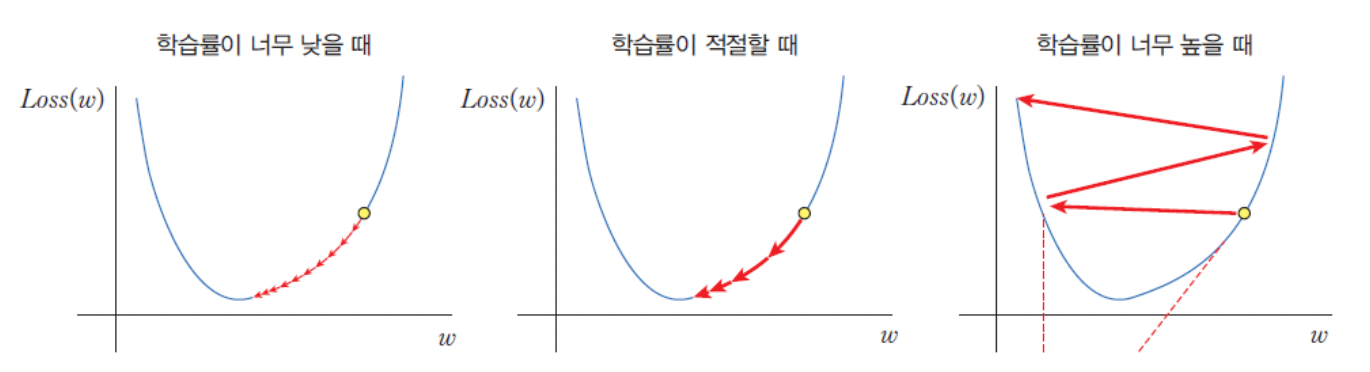
학습률 (learning rate)
: 기울기의 반대방향으로 한 번에 이동하는 정도
경사하강법 단점
1. 데이터가 많아질수록 계산량 증가
: 학습 데이터의 양이 늘어나는 경우, 계산량이 매우 커져 학습 속도가 느려진다.
2. Local Minimum 문제

: 실제 손실 함수는 위 그래프처럼 매끈하지 않고, 울퉁불퉁하기 때문에 실제로 찾아야 하는 전역 최적해(Gloabal Minimum)가 아닌 지역 최소해(Local Minimum)를 찾을 수 있다.
🎯 과잉 적합(overfitting)과 과소 적합(underfitting)
| 과잉 적합 (overfitting) | - 학습하는 데이터에서는 성능이 뛰어나지만 새로운 데이터(일반화)에 대해서는 성능이 잘 나오지 않는 모델을 생성 |
| 과소 적합 (underfitting) | - 학습 데이터에서도 성능이 좋지 않은 경우 - 모델 자체가 적합하지 않은 경우가 많다. - 더 나은 모델을 찾아야 한다. |
'🚀 What I Studied > AI' 카테고리의 다른 글
| [AI] KERAS (0) | 2022.10.29 |
|---|---|
| [AI] Perceptron (0) | 2022.10.28 |
| [AI] Machine Learning (0) | 2022.10.27 |
