티스토리 뷰
데이터사이언스를 위한 통계학입문Ⅰ
https://pabi.smartlearn.io/courses/course-v1:POSTECH+DSB111+P2203/about
데이터사이언스를 위한 통계학입문Ⅰ
pabi.smartlearn.io
II. 빅데이터 탐색의 첫걸음
2.1 데이터의 평균 (중심위치)
평균
- 데이터를 하나의 값으로 표현한 요약된 정보 (추정치)
- 평균 = 데이터 값의 총 합 / 데이터 개수
- 평균을 다룰 때 주의할 점
- 평균은 혼자 존재하는 개념이 아니다.
- 어떻게 표본선정을 하느냐에 때라 평균값에 영향을 미친다.
따라서 조사된 평균값이 모집단을 대표하는 통계치라고 할 수 있는지에 대한 고려가 필요
- 평균과 표본 산정
1. 편의 (Bias)가 적은가?
- 표본을 추출할 때 표본으로부터 얻어지는 통계치(표본평균)의 기대값이 모수의 참값과 유사한가?
2. 정확도(Precision)가 높은가?
- 반복해서 표본을 추출할 때 얼마나 유사한 값들이 나오는가?

- 평균과 분산
- 같은 평균이라도 분산이 다르면 데이터 특성은 다르다
📌요약
- 평균(mean) : 표본이 적은 경우 아주 큰 값이나 작은 값(outlier)에 민감한 추정치,
중앙값이 평균보다 더 적합한 중심 척도인 경우도 있다.
- 중앙값(median) : 데이터의 수가 작고 이상치(outlier)가 있을 때 평균보다 더 정확한 모집단의 중심값이 됨
- 최빈값(mode) : 데이터의 수가 많아질수록 평균과 가까워짐
2.2 데이터의 분산 (산포정도)
분산
- 데이터의 평균과 데이터들의 거리의 합
- 데이터의 산포정도가 크다
= 데이터가 중간에 몰려있지 않고 멀리 퍼져있다.
= 데이터가 중심위치로부터 멀리 퍼져있다.
= 데이터의 평균과 데이터들의 차이가 크다.

초록색 그래프의 분산이 가장 크고 노란색 그래프의 분산이 가장 작다.

데이터가 평균으로부터 대칭적으로 존재할 경우 편차들의 합이 0이 된다.
-> 편차를 제곱하여 더함
편차 제곱의 합을 (n-1)로 나눈다.
-> 평균값으로 표본평균을 사용하므로 1개의 자유도를 잃게되기 때문에 (n-1)로 나눈다.
표준편차
- 분산에 제곱근을 취해 원래 단위로 복원
2.3 데이터와 빅데이터
데이터
'구조화'된 데이터를 의미
ex) 다차원 배열 (matrix), 스프레드시트
데이터화 (Datafication)
- 기계가 읽어들일 수 있는 모든 것(숫자, 이미지, 텍스트)을 데이터로 변환하는 것
- 개인의 활동을 실시간으로 추적해 이를 예측 분석이 가능한 수량화된 오라닝ㄴ 데이터로 변환하는 것

빅데이터의 5V
Volume (양)
Velocity (속도)
Variety (다양성)
Veracity (정확성)
Value (가치)
빅데이터 활용사례
- MLB의 머니볼이론 및 데이터 야구

머니볼 이론이란?
머니볼: 불공정한 게임을 승리로 이끄는 과학(Moneyball: The Art of Winning an Unfair Game)
- 경기 데이터를 분석해 데이터를 기반으로 선수들을 배정 -> 승률 높임
2.4 데이터 탐색의 첫 걸음
- 데이터로 무엇을 할 수 있을까?
1. 통계치로 인사이트를 얻는다.
2. 최적의 의사결정 - 1) 데이터 탐색
ex) 공정에 대한 평균, 산포, 불량률을 추정
-> 품질의 변동상황을 관리도(Control Chart)로 표현
-> 공정에 발생하는 이상요인을 빨리 탐지하여 수정조치를 취함으로써 불량품 발생을 사전에 억제 가능
2. 최적의 의사결정 - 2) 통계적 품질관리

관리도 차트에서 봐야할 것은
관리 상한선, 관리 하한선을 어떻게 결정할 것인가?

3. 데이터의 숨겨진 패턴을 분석 - 분류
ex) 이미지 분석을 통한 의료진단 및 헬스케어
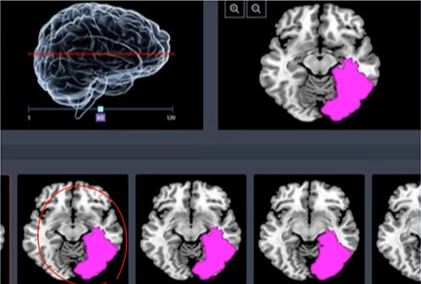
- 암과 정상인 뇌 영상을 숫자화 (데이터화)
-> 분류를 가장 잘 구분하는 변수를 찾고 범주 간의 차이를 가장 잘 표현하는 새로운 함수를 구함
-> 새로운 환자의 영상을 보고 어느 범주에 더 가까운지 판별하여 암 여부 진단
- 각 영상은 p개의 변수들로 이루어지며, 범주 1(암) 또는 범주 2(정상) 중 하나에 속함
- 변수들의 선형 조합으로 새로운 변수 Z를 형성 후 이를 바탕으로 분류 규칙을 만듦
Z = w1X1 + w2X2 + ... + wpXp = w^T*x
- 두 범주가 잘 분류된다는 것은 두 범주가 겹치지 않으면서 두 범주의 중심위치가 가능한 멀리 위치
-> 즉, 범주 간 Z의 (범주 간 Z의 평균차이 / Z의 분산) 값이 최대화 되는 w값을 찾는 것이 목적
4. 웹 마이닝을 통한 트렌드 분석
- Weighted Moving Average를 통한 트렌드 파악
-> 과거 트렌드를 반영하되 먼 과거의 데이터보다 가까운 시점의 데이터를 더 중요시함
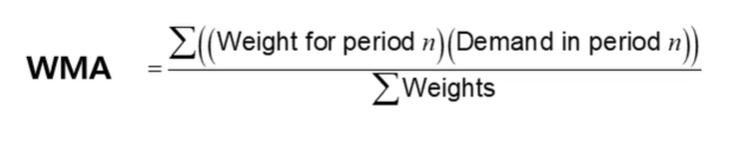

위 그래프에서 볼 수 있듯 지난 달의 데이터에는 가중치 3을 곱하고, 2달 전 데이터에는 2, 3달 전 데이터에는 1과 같이
가까운 시점의 데이터를 중요시 한다는 것을 알 수 있다.
'🚀 What I Studied > Statistics' 카테고리의 다른 글
| [Statistics] 현업 데이터 특성과 예측 모형 (1) | 2022.10.05 |
|---|---|
| [Statistics] 통계검정방법 (1) | 2022.09.26 |
| [Statistics] 빅데이터 분석에서 확률과 분포 (0) | 2022.09.20 |
| [Statistics] 데이터 시각화와 통계적 해석 (0) | 2022.09.18 |
| [Statistics] 데이터 과학과 통계 (0) | 2022.09.07 |
