티스토리 뷰
데이터사이언스를 위한 통계학입문ⅠI
https://pabi.smartlearn.io/courses/course-v1:POSTECH+DSB112+P2203/about
데이터사이언스를 위한 통계학입문Ⅱ
pabi.smartlearn.io
V. 통계검정방법
5.1 신뢰구간의 의미
신뢰구간 : 구간추정
- 실제 모수가 존재할 가능성이 높은 구간으로 추정
- 모평균, 모비율 등 모수를 포함할 확률
- 신뢰수준(Confidence level) : 구간에 모수u가 포함될 확률
- 일반적으로 100(1-a)%로 나타냄

95% 신뢰구간의 의미
1) 100번의 반복샘플링을 통해 얻은 평균과 편차로 계산한 100개의 신뢰구간 중 5개는 실제모평균(u)을 포함하고 있지 않는다.
2) 표본을 통해 얻은 95% 신뢰구간에 실제 모평균이 포함되지 않을 확률은 5%이다

몇 퍼센트의 신뢰구간이 적당한가?

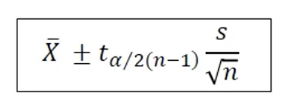
여론조사에서 95% 신뢰구간을 사용하는 이유는 무엇일까
-> 오차범위를 3% 내외로 사용하기 위해

표본사이즈와 허용오차
: 허용오차를 일정수준으로 정하면 그에 따른 표본크기가 정해진다.
-> 실험 및 조사설계를 할 때 허용오차 및 신뢰수준을 고려해야 정확한 분석이 가능하다.
5.2 통계적 검정은 왜 필요한가
통계적 검정이란?
가설의 진위 여부를 판단, 증명, 검정하는 통계적 추론 방식
1. 귀무가설(H0)
- 검정 대상이 되는 가설
- 기각을 목표로 함
2. 대립가설(H1)
- 귀무가설이 기각될 때 받아들여지는 가설
- 채택을 목표로 함
가설 검정의 절차
: 가설 설정 -> 유의수준 설정 -> 검정통계량 산출 -> 가설 기각/채택
검정 예시 : T-test

단측검정 예시
-> (소비자 주장) 카페에서 파는 커피용량이 200ml보다 적다
귀무가설(H0) : 커피의 용량은 200ml다
대립가설(H1) : 커피의 용량은 200ml보다 적다
T-분포를 이용한 검정
: 한집단 혹은 두 집단 간 평균 차이에 대한 통계적 검정 방법
T-distribution
- 많은 사회 현상은 평균 데이터가 많기 때문에 정규 분포의 형태
- 정규 분포는 표본의 데이터 수가 많아야 신뢰도 향상(일반적으로 30개 이상)
- 데이터가 적은 경우 예측 범위가 더 넓은 T-distribution 사용
T-test의 가정
- 독립성 : 두 집단의 변수는 서로 독립
- 정규성 : 두 집단의 데이터는 정규분포를 만족
- 등분산성 : 두 집단의 분산은 동일

5.3 두집단 t-검정
두 모집단의 평균을 비교하기 위한 t-검정의 계산 과정을 익힌다.
- 두 집단간 평균비교
목적 : 수면 장애가 있는 환자들에게 a,b 약제를 투여하여 그 효과를 비교하고자 한다. 투약했을 때 수면시간 증가에 유의한 차이가 있는지 조사

- 데이터로 부터 얻은 기술통계치
A에 대한 평균 : 0.75, 분산 : 3.6
B에 대한 평균 : 2.33, 분산 : 4.0
가설 : 약물종류(A,B)따라 환자의 평균 수면시간 증가에 차이가 있는지 유의수준 5%에서 검정

T-검정의 검정통계량과 기각역
두 모집단의 분산이 동일하다고 할 때 평균 수면시간 증가량에 차이가 있는지 유의수준을 5%에서 검정
약물a에 대한 데이터 수 : 10, 평균 : 0.75, 분산 : 3.6
약물b에 대한 데이터 수 : 10, 평균 : 2.33, 분산: 4.0

검정통계량

검정통계량이 기각역 안에 있으면 귀무가설을 기각 -> 대립가설을 인정

통계검정결과에 대한 결론
- A,B 투약 후 수면시간 증가에 유의한 차이가 있는지 조사
유의수준 0.05에서는 귀무가설을 기각할 수 없음
-> 유의수준 0.05에서 약물 A와 약물 b간 수면시간 증가에 유의한 차이가 없다
그러나, p-value 0.086은 < 0.1이므로 B약제의 효과가 유의수준 0.1에서는 유의하다고 볼 수 있다.
5.4 p-value의 실제 의미
p-value는 변수의 유의성 정도 혹은 검정의 유의도를 나타내준다.

분산분석 예제에서의 p-value
Type 1 error : H0가 참인데 기각
Type 2 error : H0가 거짓인데 채택

즉, p-value는 가설 채택/기각에 대한 정도

'🚀 What I Studied > Statistics' 카테고리의 다른 글
| [Statistics] 현업 데이터 특성과 예측 모형 (1) | 2022.10.05 |
|---|---|
| [Statistics] 빅데이터 분석에서 확률과 분포 (0) | 2022.09.20 |
| [Statistics] 데이터 시각화와 통계적 해석 (0) | 2022.09.18 |
| [Statistics] 빅데이터 탐색의 첫걸음 (1) | 2022.09.16 |
| [Statistics] 데이터 과학과 통계 (0) | 2022.09.07 |
