티스토리 뷰
데이터사이언스를 위한 통계학입문Ⅰ
https://pabi.smartlearn.io/courses/course-v1:POSTECH+DSB111+P2203/about
데이터사이언스를 위한 통계학입문Ⅰ
pabi.smartlearn.io
IV. 빅데이터 분석에서 확률과 분포
4.1 확률의 기초개념
통계
: 데이터를 수집, 처리, 분석, 활용하는 지식
-> 실제 얻어진 데이터를 바탕으로 정보를 도출
확률
: 어떤 특정한 사건이 일어날 가능성을 0과 1사이의 값으로 나타낸 것
-> 관측하기 전에 있어서 가능성을 논하는 것
통계에서 필요한 확률 - 확률, 사건, 표본공간
확률 : 어떤 특정한 사건이 일어날 가능성을 0과 1사이의 값으로 나타낸 것
사건 : 표본공간에서 관심의 대상인 부분집합
표본공간 : 확률 실험의 모든 가능한 결과의 집합

- 합집합 사건 : 사건 A 또는 사건 B가 일어날 때, P(AUB) = P(A) + P(B) - P(A∩B)
- 교집합 사건 : 사건 A와 사건 B가 동시에 일어날 때, P(A∩B)
- 여집합 사건 : 표본공간 S에서 사건 A가 일어나지 않을 때, P(AC) = 1 - P(A)
- 배반사건 : 교집합 사건이 공사건일 때, 사건 A와 B가 서로 배반 (mutually exclusive)
통계에서 필요한 확률 - 확률변수와 기대값
확률변수 : 확률 실험으로부터 나타난 결과에 실수를 할당한 함수
기대값 : 확률변수의 중심척도로, 어떤 랜덤한 상황에서 수치로 나타난 결과가 A1, A2, ..., Ak 이고 각 결과의 확률이 P1, P2, ..., Pk 이면 기대값은 각 결과에 확률을 곱하여 전부 합한 것
기대값 = A1P1 + A2P2 + ... + AkPk
예제)
앞면이 나올 확률이 1/2인 동전을 3번 던진다고 할 때, 확률변수 X를 앞면의 수라고 정의하자.
이 때 확률변수 X가 취할 수 있는 값은 0,1,2,3이다. 각각에 해당되는 확률과 기대값을 구하시오.

4.2 조건부 확률과 베이즈 확률
조건부 확률과 통계적 독립
조건부 확률(conditional probability)
: 어떤 사건(B)에 발생한다는 조건 하에서 다른 사건(A)이 발생하게 될 확률
P(A|B) = P(A)일 때, 즉 사건 B가 일어난다는 정보가 사건A의 발생에 전혀 영향을 주지 않을 때,
두 사건이 통계적 독립(independent)

베이즈 정리 (Bayes' Theorem)
- 주어진 (사전정보) 가설에 새로운 정보(B)가 주어졌을 때 사후확률을 계산


예제)
보험회사의 빅데이터 자동 시스템 분석 프로그램에서 사기(fraud)사건으로 의심되면 사기여부에 대한 실제 조사가 실시된다. 실제로 사기사건 확률은 p(F)=0.15, 사기사건이 아닌 확률은p(F not)=0.85이다. 그리고 실제 사기사건에 대한 정보(가능도)p(Pos|F)=0.95, p(Pos|not F)=0.01가 경험적으로 주어져 있다.
p(F) = 0.15, p(F not) = 0.85, p(Pos|F) = 0.095, p(Pos|not F) = 0.01
이 때 자동시스템에서 어떤 보험사건이 사기사건이라고 나온 경우, 실제 그 사건이 '보험사기' 건일 확률은 얼마일까
풀이)
구하고자 하는 확률은
P(F : 실제 사기사건 | Pos : 자동시스템에서 'positive'로 분류)
= {P(F) * P(Pos|F)} / {P(F)*P(Pos|F) + P(not F)*P(Pos|not F)}
= (0.15)(0.95) / (0.15)(0.95) + (0.85)(0.01)
= 0.9437
따라서 해당 사건은 확률값이 0.9437이므로 사기사건이라고 분류할 수 있다.
📌요약
- 조건부 확률이란 어떤 사건이 발생한다는 조건 하에서 다른 사건이 발생하게 될 확률
- 베이즈 정리란 사후확률을 사전확률과 가능도를 이용하여 계산할 수 있도록 해주는 확률 변환식
- 머신러닝기법 중 '나이브베이즈 분류' 기법 계산에서 베이즈 정리가 활용
4.3 정규분포(연속형)와 포아송분포(이산형)
확률분포란?
이산형 - discrete
연속형 = continuous


이산형 분포
: 확률변수가 이산형일 때의 확률분포
기대값 E(X) = Σx * p(x)
분산 Var(X) = E(X^2) = E(X) ^ 2
ex ) 이항분포, 다항분포, 초기하분포, 포아송분포 ...
이항분포
: 어떤 시행의 결과가 단순히 '성공' 또는 '실패'로 나타날 수 있을 때 (베르누이 시행), '성공'이 나오는 횟수에 대한 확률분포
포아송 분포
: 단위 시간 안에 어떤 사건이 몇 번 발생하는가에 대한 확률분포
일정한 시간 또는 공간 내에서 발생하는, 사건의 발생횟수에 따른 확률

포아송 분포는 현실세계의 문제와 밀접한 관련이 있다.
ex)
- 일정 주어진 시간 동안에 도착한 고객의 수
- 일정 주어진 생산시간 동안 발생하는 불량의 수
- 1km 도로에 있는 흠집의 수

연속형 분포
: 확률변수가 연속형(continuous)일 때의 확률분포
- 연속형 분포에서는 정규분포(Normal distribution)가 가장 중요
- 모집단의 분포가 정규분포를 가진다고 가정하면 여러가지 통계분석이 쉬워진다.
- 실제로 사회적, 자연적 현상의 통계치들의 분포가 정규분포와 비슷한 형태를 띈다.

정규분포는 평균을 중심으로 대칭을 이루는 종모양의 연속확률분포
연속형 분포 - 표준정규분포
- 표준정규분포는 평균이 0이고 분산이 1인 정규분포


연속형 분포 - 카이제곱분포

연속형 분포 - F-분포

4.4 데이터에서 출발하는 확률과 분포
중심극한정리 (Central Limit Theorem)
- 이항분포에서 표본의 수가 증가함에 따라 표본들의 전체 합이 점점 정규분포에 근접
지수 분포
: 지수 분포에서도 표본의 수가 증가함에 따라 표본 평균의 분포는 점점 정규분포와 비슷해진다.

-> 원래의 분포가 정규분포가 아니더라도 표본의 수가 증가함에 따라 표본평균이 점점 정규분포 모형과 비슷해진다.
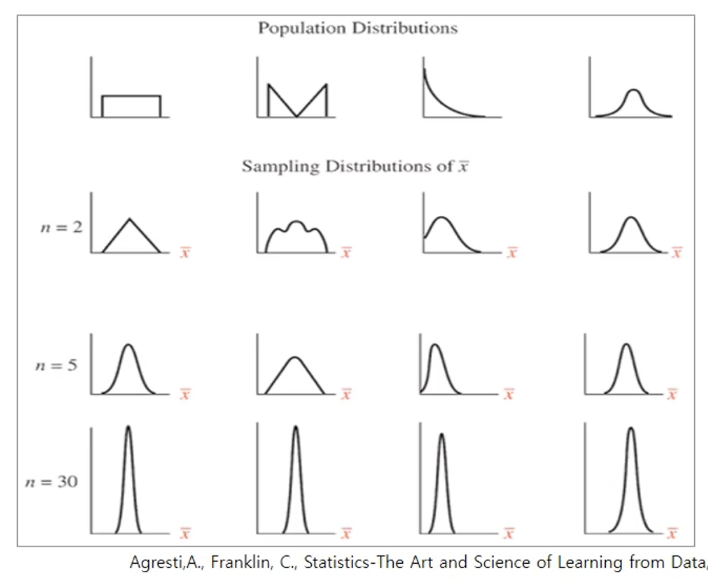
- 평균이 u이고 분산이 σ ^2인 모집단으로부터 크기 n인 확률표본을 추출할 때, n이 크면 표본평균 X바 는 N(u, σ ^2/n) 에 근접
- 보통 n이 30이상이면 모집단의 분포에 관계없이 X바는 정규분포에 근사
중심극한정리가 유용한 이유
: 대부분의 통계적 검정과 추정은 모집단이 정규분포를 따른다는 가정 하에서 이루어짐
-> 모집단의 분포를 몰라도 중심극한정리를 이용하면 표본평균의 통계적 검정과 추정이 가능해진다.
끝!

'🚀 What I Studied > Statistics' 카테고리의 다른 글
| [Statistics] 현업 데이터 특성과 예측 모형 (1) | 2022.10.05 |
|---|---|
| [Statistics] 통계검정방법 (1) | 2022.09.26 |
| [Statistics] 데이터 시각화와 통계적 해석 (0) | 2022.09.18 |
| [Statistics] 빅데이터 탐색의 첫걸음 (1) | 2022.09.16 |
| [Statistics] 데이터 과학과 통계 (0) | 2022.09.07 |
