티스토리 뷰
데이터사이언스를 위한 통계학입문Ⅰ
https://pabi.smartlearn.io/courses/course-v1:POSTECH+DSB111+P2203/about
데이터사이언스를 위한 통계학입문Ⅰ
pabi.smartlearn.io
III. 데이터 시각화와 통계적 해석
3.1 데이터 시각화
데이터 시각화
: 데이터 분석 결과를 쉽게 이해할 수 있도록 보여주는 것
데이터 분석 단계
- 수집 (Data Gathering)
- 정제 (Data Processing)
- 시각화 (Data Visualization)
- 예측모형/분석 (Data Analysis)
효과적인 데이터 시각화의 조건
- 어떤 메세지를 전달할 것인지 결정 (what)
- 핵심 내용을 제외한 나머지는 생략
- 최선의 표현 방법을 선택 (How)
- 단순, 명료하게 디자인 (How)
- 데이터를 토대로 어떤 의사결정을 해야 하는지에 대해 설명 (why)
3.2 그래프의 유용성과 오류
그래프의 유용성 예제

히스토그램으로 보면 같은 분산이라도 데이터의 분포를 더 잘 파악할 수 있다.

이상치(Outlier)의 존재도 파악 가능
히스토그램 주의 사항
- 계급 구간을 어떻게 설정하는지에 따라 히스토그램 그래프가 완전히 달라진다.

y축의 설정에 따라서도 전혀 다른 그래프가 나타난다.
📌요약
그래프의 목적은 데이터를 분명하게 표현하는데 있다.
1. 그래프를 작성할 때는 축의 범위, 간격 등을 잘 정해야 한다.
2. 그래프를 보는 사람의 수준을 고려해야 한다.
3. 그래프 종류별 장점과 단점을 정확히 파악하고 사용해야한다.
3.3 상자그림이 주는 정보와 해석
왜 상자 그림이 필요한가?
- 기술통계치(평균, 분산)만으로는 데이터에 대해 잘 알 수가 없다.
- 평균, 분산을 안다고 데이터가 어느 쪽에 더 많이 분포하는지 알 수 없다
- 이상치가 존재하는지 알 수 없다
- 데이터의 분포 범위(최대값, 최소값)를 한눈에 알기 어렵다.
상자그림이 주는 정보 5가지
- 중앙값, 일사분위수, 삼사분위수, 최대값, 최소값
일사분위수(Q1) : 데이터를 크기순서로 배열했을 때 25% 지점의 값
삼사분위수(Q3) : 데이터를 크기순서로 배열했을 때 75% 지점의 값

-> 데이터 분포의 대칭성, 치우침, 이상치를 쉽게 파악 가능
상자그림을 그리는 방법
1. 데이터의 중앙값(median)을 찾는다.
2. 일사분위수와 삼사분위수를 갖는다.
3. 일사분위수 ~ 삼사분위수를 상자로 그린다. (사분위범위)
4. 최소값 ~ 일사분위수, 삼사분위수 ~ 최대값을 그린다.
5. 이상치 표시
- 일사분위로부터 -(1.5)*사분위범위를 넘는 관측치는 이상치로 표시
- 삼사분위로부터 +(1.5)*사분위범위를 넘는 관측치는 이상치로 표시
3.4 산점도와 상관관계 - 트렌드 분석
산점도(Scatter plot)
: 변수 간 관계의 방향, 트렌드, 강도를 살펴볼 수 있는 그래프
-> 여러 변수들 사이의 관계를 볼 때는 산점도 필요
산점도로부터 알 수 있는 3가지
- 트렌드 : linear, curved, clusters, no pattern
- 방향 : positive, negative, no direction
- 강도 : how closely rhe points fit the trend
산점도의 해석 - 방향

- 두 변수 X와 Y가 X값이 클 때 Y값도 큰 경향이 있고, X값이 작을 때 Y값도 작은 경향
-> 양의 상관관계 (positively associated)
- 두 변수 X와 Y가 X값이 클 때 Y값도 작은 경향이 있고, X값이 작을 때 Y값도 큰 경향
-> 음의 상관관계 (Negatively associated)
상관계수 (Correlation, r)
- 상관관계의 강도를 나타낸다.
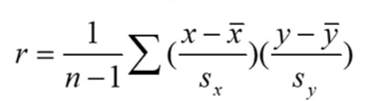
r은 -1부터 +1까지 존재하며,
+1에 가까울수록 강한 양의 상관관계,
-1에 가까울수록 가한 음의 상관관계
산점도에서 상관관계란 선형적인(linear) 상관관계만 의미
📌요약
- 산점도는 두 변수 간 관계의 방향, 형태, 강도를 살펴볼 수 있는 그래프
- 상관계수(r)는 두 변수 간 선형적인 상관관계의 강도를 나타낸다.
- 산점도에서 선형모형(선형함수식)을 구현할 수 있다.
'🚀 What I Studied > Statistics' 카테고리의 다른 글
| [Statistics] 현업 데이터 특성과 예측 모형 (1) | 2022.10.05 |
|---|---|
| [Statistics] 통계검정방법 (1) | 2022.09.26 |
| [Statistics] 빅데이터 분석에서 확률과 분포 (0) | 2022.09.20 |
| [Statistics] 빅데이터 탐색의 첫걸음 (1) | 2022.09.16 |
| [Statistics] 데이터 과학과 통계 (0) | 2022.09.07 |
